Satranç ve matematik | Evrensel Bilgin

Satranç ve matematik arasında ayrılmaz bir bağlantı olduğu çok açıktır. Peki, satranç sadece matematikle açıklanabilir mi? Özünde soyut olan matematiğin zaman zaman satranç tahtasında somut hale geldiğini görsek de satrancı salt matematikle açıklamak mümkün değildir. Ancak sınırlı sayıda kare ve sınırlı sayıda taşla ortaya çıkan olası oyunların muazzam sayısı oyunun karmaşıklığı ile birleştiğinde kaçınılmaz olarak matematikseldir de.

Matematiği bir oyunla ilişkilendirmek genellikle olasılıkla ilgilidir. Poker ve benzeri oyunlarda olasılıkların çok önemli olması, şans ve bilginin rakipten gizlenmesiyle harmanlanır. Oysa satrançta rastlantı ve gizli bilgi yoktur.  Satranç oyunu sırasında taşlara sayısal değerler vererek oyunun kimin kazanacağını anlamak genellikle mümkündür. Genellikle diyorum, çünkü satranç oynarken taşların değerlerinin değiştiğine şahit oluruz. Oyuncu rakip atı ele geçirmek için iki piyon feda ettiğinde atın genel olarak üç piyon değerinde olduğunu bildiğinden bunu avantajlı bir alışveriş olarak sayar. Ancak oyun sonunda iki piyon attan değerli de olabilir. Oyuncu bu problemi çözmekte matematiği yardımcı olmak için kullanabilir.

Satranç çok acımasız bir oyundur. Oyunun bir bölümüne kadar mükemmel oynamış olabilirsiniz ancak yapacağınız tek bir küçük hata oyunu kaybetmenize neden olabilir. Amatörlerin oyunlarında ibre bir o yana bir bu yana kaysa da usta seviyesinde ikinci şans diye bir şey yoktur. Oyun sırasında zihnimiz sürekli olarak tahtada tarama yaparak olası çözümleri bir araya getirmeye çalışır. Satranç, olasılıkları ya da örüntüyü keşfetmeniz için sizi zorlar. Herhangi bir konumda yapmak istediğiniz hamle ile konumun sizden yapmanızı beklediği hamle arasında gidip gelirsiniz. Çoğunlukla çözüm tümevarımla bulunsa da tümdengelim adeta beklenmedik bir sol kroşe etkisi yaratır.

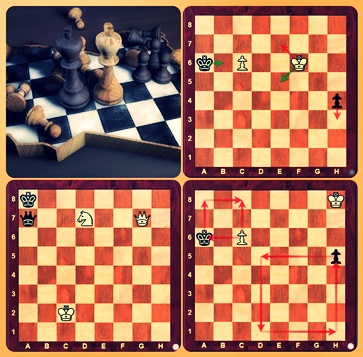
Yıllar önce aşağıdaki konumla karşılaştığımda beyazın nasıl kazanması gerektiğini düşünürken sürekli bir sonraki hamleyi hesaplamaya çalışıyor ve bir süre sonra varyantların arasında kayboluyordum.

Sonra problemi tümdengelimle çözmenin doğru olabileceğini düşünerek son konumun ne olması gerektiğini buldum. Bunu yaparken satrancın sihirli kelimesi olan “eğer”i kullandım. Eğer şah burada ve eğer vezir burada olsaydı kazanırdım gibi. İlk konumla son konumun arasındaki en belirgin fark rakip vezirin bir sıra aşağıda olmasıydı. Diyagram.

İşte kazanan konum. Peki, bu konuma nasıl ulaşacağız? Tabii ki zorunlu hamleler dizisiyle. İlk konumu tahtaya dizip aşağıdaki hamleleri oynayarak vezirin tahtanın geometrisini nasıl kullandığını görmenizi tavsiye ederim. 1.Vg2+ Vb7 2.Vg8+ Şa7 3.Vg1+ Şa8 4.Va1+ Va7 5.Vh1+ Vb7 6.Vh8+ Şa7 7.Va1+ Va6 8.Vg1+ Şa8 9.Vg8+ Şa7 [9…Şb7 10.Ac5+ çatalla vezir kazanır] 10.Vb8#

Satrançta özellikle oyun sonunda matematiğe ihtiyacımız artar. Tahtada daha az taş ve kesin hesaplama gerektiren konumlar oluşur. Richard Reti, 1921 yılında yayımladığı kurgu ile geometrinin babası sayılan Öklid’in şapkasından tavşan çıkartmıştır. Diyagram, Beyaz oynar beraberlik.

Kare kuralına göre beyaz piyonun siyah şah tarafından kontrol edildiğini, diğer yandan beyaz şahın siyah piyonun terfisine engel olamayacağını görüyoruz. O zaman beraberlik nasıl mümkün olabilir? Burada bizi yanıltan satranç tahtasının geometrisi ile taşların hareketleri arasındaki uyumsuzluk. Gözümüz h8 ile a8 arasındaki mesafenin h8 ile a1 arasındaki mesafeden kısa olduğunu söylüyor. Ne var ki bu durum h8’deki şahın pek de umurunda değil. Çünkü onun için a8’e ya da a1’e gitmek arasında hiçbir fark yok, ikisi de yedi hamledir. Tez; rakip piyonun terfisini durdurmak. Antitez; kendi piyonumun terfisine yardım etmek. Sentez; her iki planı içeren ve şartlara göre esnek olabilen hamle dizisini seçmek. 1.Şg7 h4 2.Şf6 Diyagram

Anahtar konum. Şimdi siyah 2…h3 oynarsa 3.Şe7! h2 4.c7 Şb7 5.Şd7 h1V 6.c8V+ Beraberlik.

Eğer siyah 2…Şb6 oynarsa 3.Şe5! h3 (3…Şxc6 4.Şf4 ve siyah piyonu yakalar) 4.Şd6 h2 5.c7 Şb7 6.Şd7 h1V 7.c8V+ ve beraberlik.

Yazarın Tüm Yazıları – Evrensel evrensel.net